The NESA Maths Reference Sheet is a superb useful resource… if you know the way to make use of it! Navigate measurement and monetary arithmetic with our Final NESA Maths Reference Sheet Information.
Whereas memorisation has its place in studying, Matrix recommends that college students be taught to derive their responses and learn to apply these formulae accurately. As a bonus, we’ve included a nifty HSC Maths Cheatsheet so that you can obtain and print out!
A free pocket-sized Maths handbook, so that you’re ready.
All the important thing Maths formulation it’s essential revise, in a single foldable cheatsheet.
We take your privateness significantly. T&Cs and Privateness Coverage.
DOWNLOAD YOUR FREE MATHS CHEATSHEET
Click on on the next formulation to see what they imply and apply them to a observe query!
| Measurement | |
| Size
(l=frac{theta}{360}times2pi r)
Space (A= frac{theta}{360} occasions pi r^2) (A=frac{h}{2} (a+b) ) |
Floor space
(A=2 pi r^2 + 2 pi r h ) (A = 4 pi r^2)
Quantity (V= frac{1}{3}Ah) (V= frac{4}{3} pi r^3) |
| Monetary Arithmetic |
| (A= P(1+r)^n)
Sequences and sequence (T_n = a+(n-1)d) (S_n=frac{n}{2} [2a+(n-1)d] = frac{n}{2}(a+l)) (T_n=ar^{n-1}) (S_n=frac{a(1-r^n)}{1-r}=frac{a(r^n-1)}{r-1}, r≠1) (S= frac{a}{1-r}, |r|<1 ) |
Measurement
Size
| Use | Components | Variables |
| Arc size of a sector
(utilizing θ in levels) |
(l=frac{theta}{360}times2pi r) | start{align*} l&= textual content{arc size} theta &= textual content{angle of sector in levels} r &= textual content{radius} finish{align*} 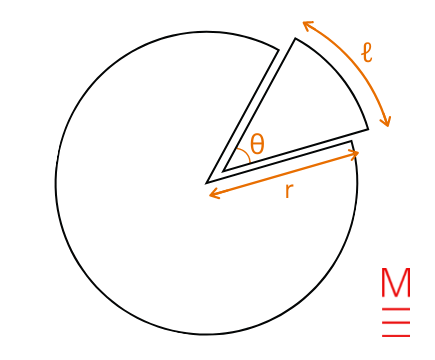 |
Again to prime
Subsequent part: Space
Instance 1:
Discover the size of the minor arc AB, such that the size of radius OA is 30 cm. Go away your reply as an actual worth.
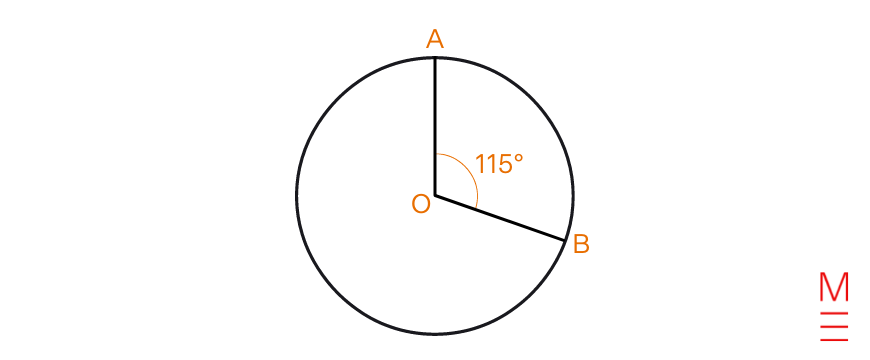
Resolution 1:
| Substitute (theta = textual content{115}) and (r = textual content{30}) into (l=frac{theta}{360}times2pi r):
start{align*} |
Again to prime
Space
| Use | Components | Variables |
| Space of a sector | (A= frac{theta}{360} occasions pi r^2) | start{align*} A&= textual content{space of sector} theta &= textual content{angle of sector in levels} r &= textual content{radius} finish{align*} 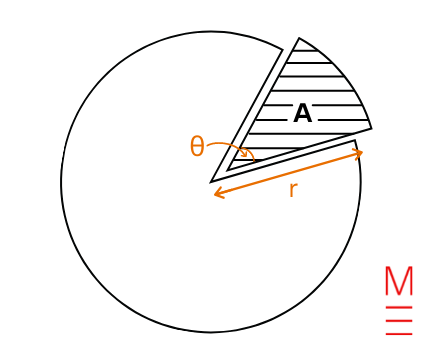 |
Again to prime
Subsequent part: Floor Space
Instance 2:
Provided that the next circle has a radius of 5 m, discover the world of the most important sector AOB. Go away your reply as an actual worth.
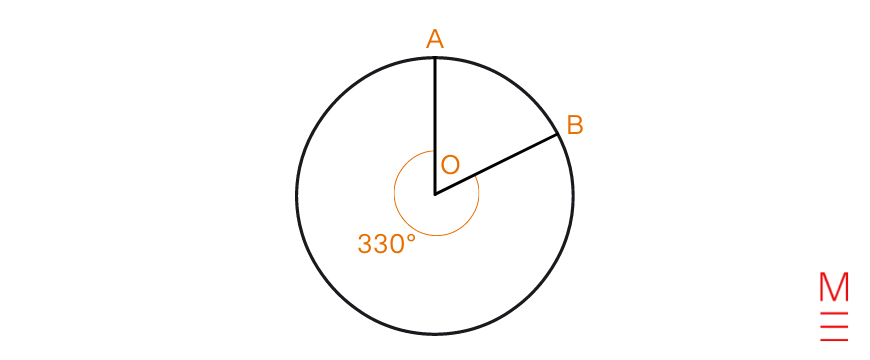
Resolution 2:
| Substitute (theta=330) and (r=5) into (A= frac{theta}{360} occasions pi r^2):
start{align*} |
Again to prime
| Use | Components | Variables |
| Space of a trapezium | (A=frac{h}{2} (a+b) ) | start{align*} A&= textual content{space of trapezium} h &= textual content{perpendicular peak} a, b &= textual content{lengths of the parallel sides} finish{align*} 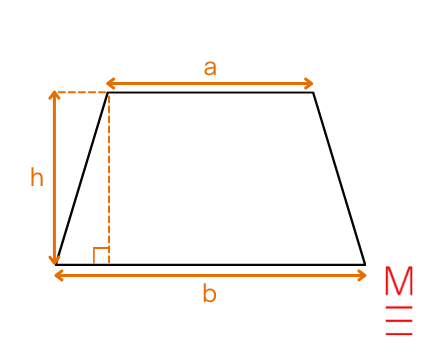 |
Again to prime
Instance 3:
What’s the space of the form under? Notice that each one the measurements have been made in millimetres.
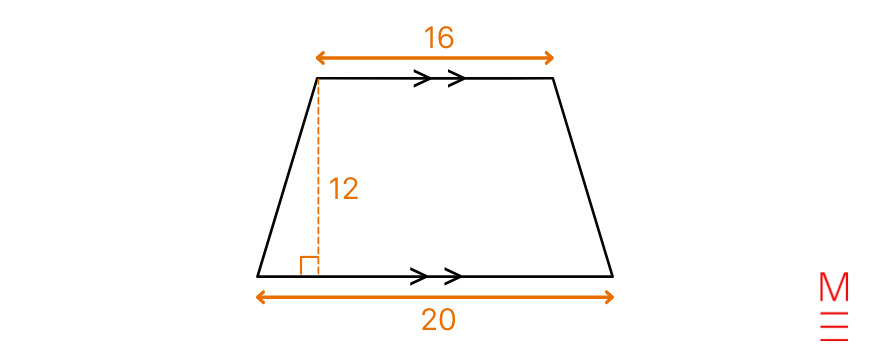
Resolution 3:
| Substitute (h=12), (a=16) and (b=20) into (A=frac{h}{2} (a+b) ):
start{align*} |
Again to prime
Floor space
| Use | Components | Variables |
| Floor space of a cylinder | (A=2 pi r^2 + 2 pi r h ) | start{align*} A&= textual content{floor space of cylinder} h &= textual content{peak} r &= textual content{radius of round base} finish{align*} 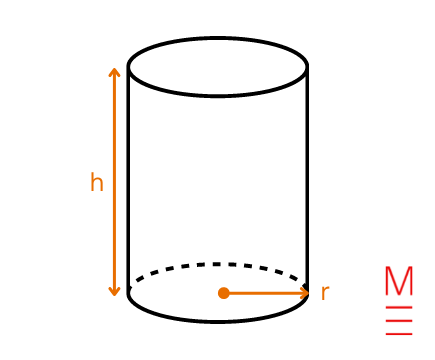 |
Again to prime
Subsequent part: Quantity
Instance 4:
Gemma is designing a can for her new spaghetti recipe. To be able to determine how a lot pink paint she must fully cowl the can, she must know what the whole floor space of the cylindrical can is.
Understanding that the scale under are given in centimetres, what’s the floor space of Gemma’s can? Go away your reply as an actual worth.
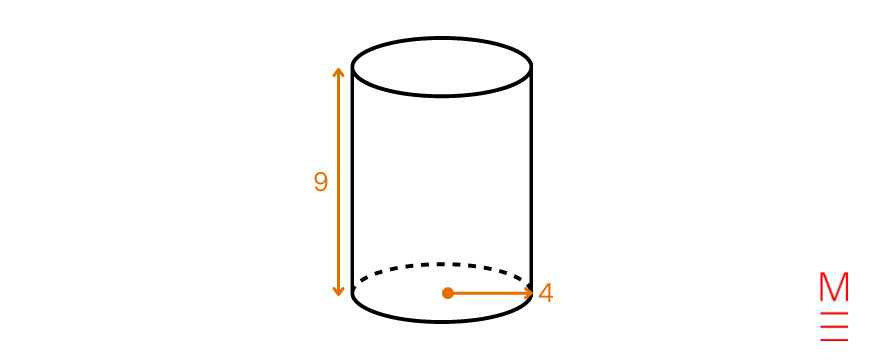
Resolution 4:
| Substitute (h=9) and (r=4) into (A=2 pi r^2 + 2 pi r h ):
start{align*} |
Again to prime
| Use | Components | Variables |
| Floor space of a sphere | (A = 4 pi r^2) |
(r = textual content{radius})
|
Again to prime
Instance 5:
Organic cells with bigger floor space to quantity ratios are capable of extra effectively diffuse oxygen into the cell and waste materials out.
If we approximate a cell to be the form of a sphere, what’s the floor space of a cell with a diameter of 0.07 mm? Go away your reply as an actual worth.
Resolution 5:
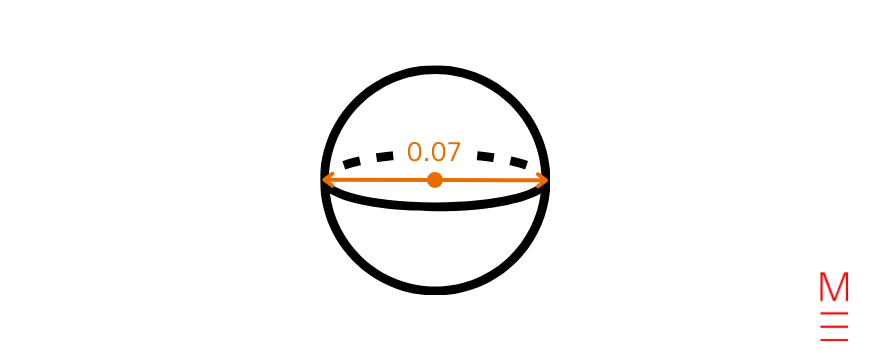
Substitute (r= frac{0.07}{2}) (because the radius is half of the diameter) into (A = 4 pi r^2): start{align*} |
Again to prime
Quantity
| Use | Components | Variables |
| Quantity of a pyramid/cone | (V= frac{1}{3}Ah) | start{align*} V &= textual content{quantity of pyramid/cone} A &= textual content{base space} h &= textual content{peak} finish{align*} 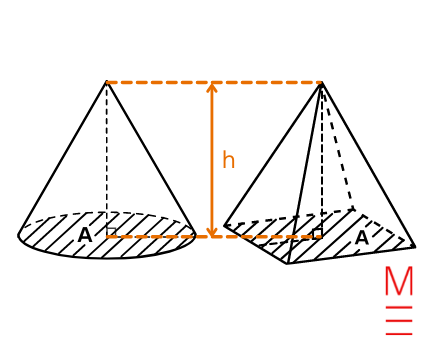 |
Again to prime
Subsequent part: Monetary Arithmetic
Instance 6:
Ricky is planning her party. She desires to prank her mates by placing water balloons inside the entire celebration hats.
Assuming that the celebration hats are an ideal cone with a radius of 5 cm and a peak of 12 cm, how a lot water does she must fill one celebration hat? Go away your reply as an actual worth.
Resolution 6:
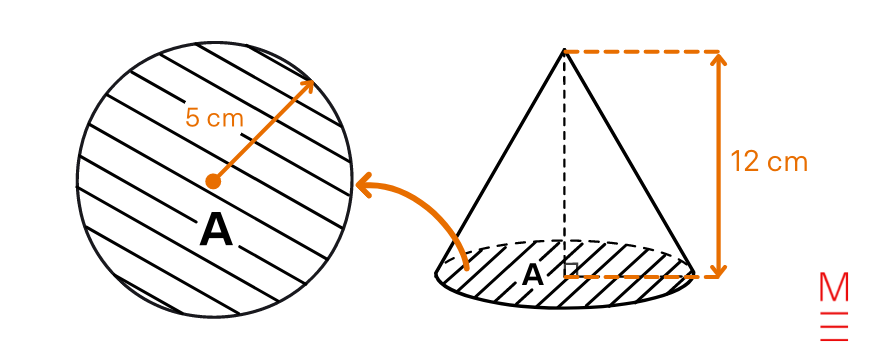
To search out the world of the round base, substitute (r=5) into (A= pi r^2): start{align*}
Substitute (A= 25 pi) and (h=12) into (V= frac{1}{3}Ah): start{align*} |
Again to prime
| Use | Components | Variables |
| Quantity of a sphere | (V= frac{4}{3} pi r^3) | (r = textual content{radius})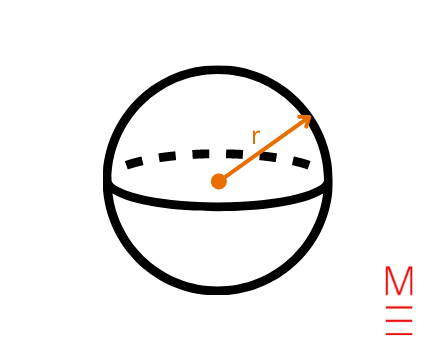 |
Again to prime
Instance 7:
Gordon is making meatballs. Assuming that 1 cm3 = 1 gram, how a lot mince does he must make a wonderfully spherical meatball with a diameter of three cm? Go away your reply as an actual worth.
Resolution 7:
| Substitute (r= frac{3}{2}) (because the radius is half of the diameter) into (V= frac{4}{3} pi r^3):
start{align*} |
Again to prime
Monetary Arithmetic
| Use | Components | Variables |
| Compound curiosity | (A= P(1+r)^n) | start{align*} A &= textual content{worth of funding on the finish of the n}^{th} textual content{ interval} P &= textual content{precept (preliminary) quantity} r &= textual content{compound rate of interest per interval — expressed as a decimal} n &= textual content{variety of time intervals} finish{align*} |
Again to prime
Subsequent part: Sequences and sequence
Instance 8:
Jacky’s financial institution is providing her a implausible rate of interest of three% every year, compounded each three months. If she deposits $12 360 into her financial savings account as we speak and resolves to not take away from or add to those funds, what can be her financial savings account steadiness in 12 months time? Present your reply to the closest two decimal locations.
Sequences and sequence
Notice: A sequence is the sum of the weather in a sequence.
Arithmetic Progressions
In an arithmetic development, every time period is decided by including a relentless to the previous time period.
| Use | Components | Variables |
| Arithmetic sequence | (T_n = a+(n-1)d) | start{align*} T_n &= textual content{n}^{th} textual content{ time period of the sequence} S_n &= textual content{sum of the primary n phrases of the sequence} n &= textual content{place of the time period} |
| Arithmetic sequence | (S_n=frac{n}{2} [2a+(n-1)d] = frac{n}{2}(a+l)) |
Again to prime
Instance 9:
Take into account the next arithmetic sequence:
( 3, 15, 27, 39… )
What’s the 23rd time period of this sequence?
Resolution 9:
| Substitute (n=23), (a=3) and (d=12) into (T_n = a+(n-1)d)
start{align*} |
Again to prime
Instance 10:
The sum of the primary 16 phrases of an arithmetic sequence is 632. Given the primary time period of the sequence is 2, write down the primary 4 phrases of the sequence.
Resolution 10:
| Substitute (S_n=632), (n=16) and (a=2) into (S_n=frac{n}{2} [2a+(n-1)d] = frac{n}{2}(a+l))
start{align*} start{align*} |
Again to prime
Geometric Progressions
In a geometrical development, every time period is discovered by multiplying the earlier time period by a relentless.
| Use | Components | Variables |
| Geometric sequence | (T_n=ar^{n-1}) | start{align*} T_n &= textual content{n}^{th} textual content{ time period of the sequence} S_n &= textual content{sum of the primary n phrases of the sequence} n &= textual content{variety of phrases being added} |
| Geometric sequence | (S_n=frac{a(1-r^n)}{1-r}=frac{a(r^n-1)}{r-1}, r≠1) | |
| Limiting sum of a geometrical sequence | (S= frac{a}{1-r}, |r|<1 ) |
Again to prime
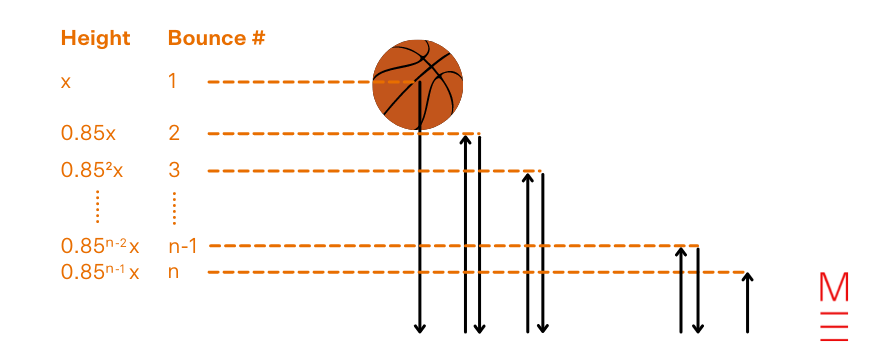
Instance 11:
A basketball participant is bouncing a ball. On every bounce, the ball reaches a peak that’s 85% of its earlier peak. The entire distance that the ball has travelled simply earlier than they make contact with the ball for the 8th time is 6 metres.
a) At what peak did the basketball participant start bouncing the ball? Give your reply in metres to the closest three decimal locations.
b) Therefore or in any other case, discover the whole distance that the ball travels if the basketball participant continues bouncing the ball till it will definitely doesn’t raise off the bottom. Give your reply in metres to the closest two decimal locations.
Resolution 11 a):
| (textual content{Let }x = textual content{preliminary bounce peak of the ball})
Let’s take into account what this drawback would appear like visually.
The peak of every bounce conveniently types a geometrical sequence the place the frequent ratio r=0.75 and the primary time period a=x. Therefore, (T_n=x occasions 0.75^{n-1}) Nevertheless, the gap that the ball travels shouldn’t be a easy geometric sequence. As you may see within the diagram above, aside from the primary bounce and last n bounce (the place the ball solely travels downwards or upwards), the ball travels twice the gap of the bounce peak because it travels up and down. Therefore, we are able to discover the whole distance d travelled by the ball earlier than the nth bounce: start{align*} On this query, we’re given the whole distance travelled by the ball earlier than the eighth bounce is 6 metres. So, substitute d=6 and n=8 into ( d = 2 occasions S_n – T_1 – T_n ): start{align*} To search out S8, substitute (a=x), (n=8) and (r=0.75) into (S_n=frac{a(1-r^n)}{1-r}): start{align*} To search out T8, substitute (a=x) and (n=8) into (T_n=ar^{n-1}): start{align*} Therefore, we are able to substitute (S_8=4[x(1-0.75^8)] ), (T_1= x ) and (T_8= x occasions 0.75^7 ) into equation 1: (6 = 2 occasions S_8 – T_1 – T_8): start{align*} |
Resolution 11 b):
| Partially a), we discovered that the whole distance d travelled by the ball is (d = 2 occasions S_n – T_1 – T_n). Want a refresher? Click on right here to scroll as much as the reason partially a).
Partially a), we have been within the distance that the ball travels earlier than the eighth bounce. So, we used (n = 8). Partially b) although, we’re looking for how far the ball can journey if it was allowed to bounce without end. So right here, we let (n = ∞). Substitute (n = ∞) into (d = 2 occasions S_n – T_1 – T_n): start{align*} Since: start{align*} start{align*} |
Evaluate ‘Collection and Sequences’ and obtain your free worksheet right here.
Again to prime
,