The NESA Maths Reference Sheet is a great resource… if you know how to use it! Navigate statistics and combinatorics with our Ultimate NESA Maths Reference Sheet Guide.
While memorisation has its place in learning, Matrix recommends that students learn to derive their responses and learn how to apply these formulae correctly. As a bonus, we’ve included a nifty HSC Maths Cheatsheet for you to download and print out!
A free pocket-sized Maths handbook, so you’re prepared.
All the key Maths formulas you need to revise, in one foldable cheatsheet.
Click on the following formulas to see what they mean and apply them to a practice question!
| Statistical Analysis |
| \(z=\frac{x-µ}{σ}\)
\(\text{An outlier is a score:}\)
Normal distribution
\(E(X)=μ=\sum xP(X=x)\) \(Var(X)=E[(X-μ)^2]=E(X^2)-μ^2\)
Probability \(P(A∩B)=P(A)P(B)\) \(P(A∪B)=P(A)+P(B)-P(A∩B)\) \(P(A|B)=\frac{P(A∩B)}{P(B)}, \ P(B)≠0\)
Continuous random variables \(P(X≤r) = \int _a^r f(x) \ dx\) \(P(a < X < b) = \int _a^b f(x) \ dx\)
Binomial distribution \(P(X=r) = \ ^n C_r p^r (1-p)^{n-r}\) \(X \text{~ Bin} (n,p)\) \(⇒ P(X=x) = \binom{n}{x} p^x (1-p)^{n-x}, \ x=0, \ 1, \ . \ . \ . \ , \ n\) \(E(X)=np\) \(\text{Var} (X) = np(1-p)\) |
| Combinatorics |
| \(^n P_r = \frac{n!}{(n-r)!}\)
\(\binom{n}{r} = \ ^n C_r = \frac{n!}{r!(n-r)!}\) \((x+a)^n = x^n +\binom{n}{1} x^{n-1} a + … + \binom{n}{r} x ^{n-r}a^r + … + a^n\) |
Statistical Analysis
| Use | Formula | Explanation |
| z-score | \(z=\frac{x-µ}{σ}\) | \(z\) = z-score
\(x\) = score \(µ\) = mean/average \(σ\) = standard deviation |
| Outliers | \begin{align*} \text{An outlier is a score:}\\ &\text{less than } Q_1 – 1.5 \times IQR\\ &\text{or}\\ &\text{more than } Q_3 +1.5 \times IQR\\ \end{align*} |
Outlier: a number/value that does not appropriately represent the data set
Q2: Median of the whole set = the middle term Q1: First quartile = the median of all the numbers smaller than the median of the whole set Q3: Third quartile = the median of all the numbers greater than the median of the whole set IQR: interquartile range = Q3 – Q1 |
Back to top
Next section: Combinatorics
Example 24:
Consider the ages of a group of individuals:
1, 2, 4, 5, 13, 14, 24, 70
a) List out all the outlier value(s).
b) After removing all outliers, calculate the z-score of the third youngest individual (nearest 2 decimal places).
Solution 24 a):
| \begin{align*} Q_1 &= \frac{2+4}{2} \\ &= 3 \\ Q_3 &= \frac{14+24}{2} \\ &= 19 \\ 1.5 \times IQR &= 1.5 \times (Q_3 – Q_1) \\ &= 1.5 \times (19 – 3) \\ &= 24 \\ Q_1 – 1.5 \times IQR &= 3 – 24 \\ &= -21 \\ Q_3 + 1.5 \times IQR &= 19 + 24 \\ &= 43 \\ \end{align*}There are no values smaller than \(Q_1\) — 1.5 IQR = -21, but there is a value greater than \(Q_3\) + 1.5 IQR = 43 < 70.Therefore, the outlier value is 70. |
Solution 24 b):
| \begin{align*} µ &= \frac{1 + 2+ 4+ 5+ 13+ 14+ 24}{7} \\ &= 9 \\ σ &= 7.746 \\ z &=\frac{x-µ}{σ} \\ &= \frac{4-9}{7.746} \\ ∴ z-score &= – 0.65 \text{ (nearest 2 decimal places)} \\ \end{align*} |
Back to top
Normal distribution
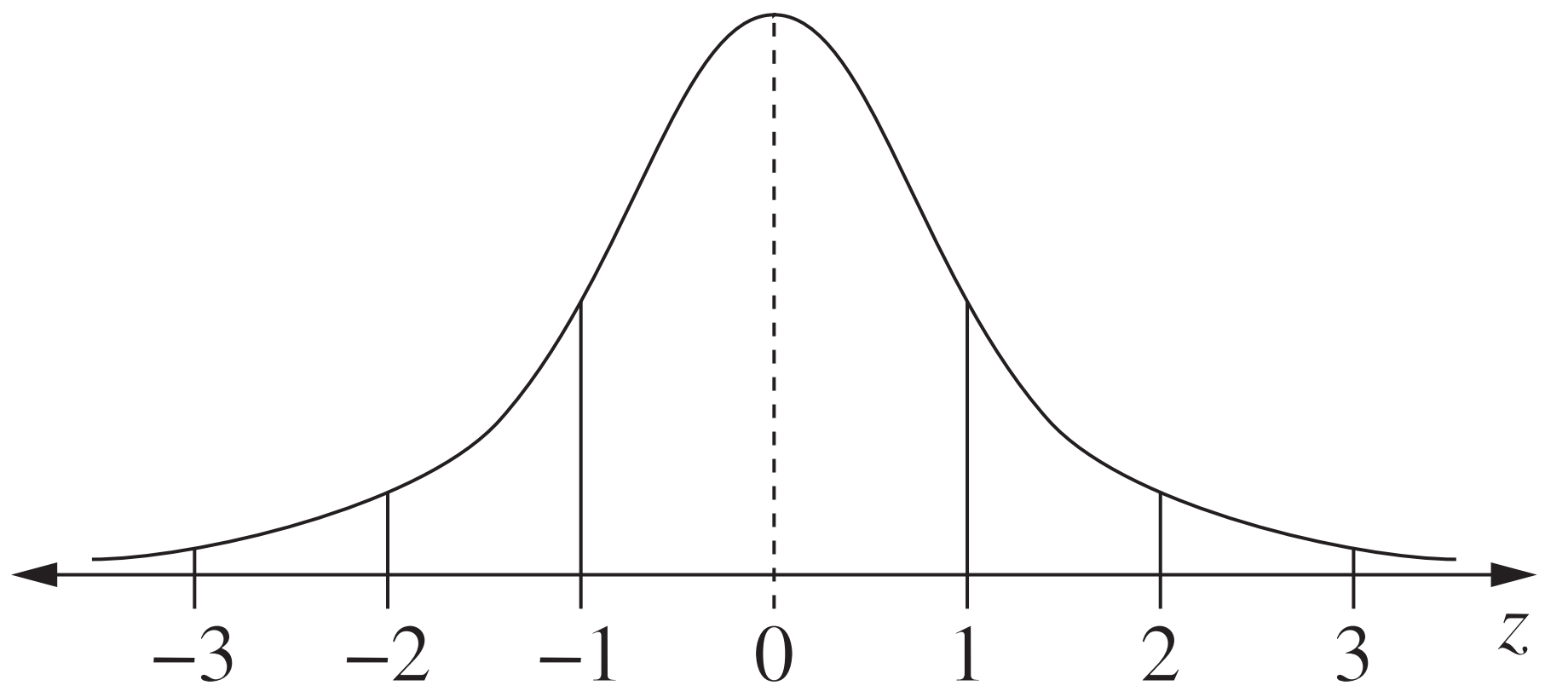
|
| Use | Formula | Variables |
| Expected value | \(E(X)=μ\) | E(X): expected value of a normal distribution
μ: mean/average of all the values in the normal distribution |
| Variance | \(Var(X)=E[(X-μ)^2]=E(X^2)-μ^2\) | Var(X): variance of a normal distribution
E(Y): mean of defined Y function μ: mean/average of all the values in the normal distribution |
Back to top
Probability
| Use | Formula | Explanation |
| Probability of both event A and event B occurring | \(P(A∩B)=P(A)P(B)\) | ∩: or
∪: and |: given A and B are events that could be defined as anything, e.g. landing heads on a coin, winning a sports match or raining the next day. |
| Probability of event A or event B occurring (this includes when both events occur) | \(P(A∪B)=P(A)+P(B)-P(A∩B)\) | |
| Conditional probability
Probability of event A occurring, given event B has occurred |
\(P(A|B)=\frac{P(A∩B)}{P(B)}, \ P(B)≠0\) |
Back to top
Continuous random variables
| Formula | Explanation |
| \(P(X≤r) = \int _a^r f(x) \ dx\) | \(a\) and \(b\) are constants ∈ \(\mathbb{R}\)
Need help with integration? See our list of guides here. |
| \(P(a < X < b) = \int _a^b f(x) \ dx\) |
Back to top
Binomial distribution
| Use | Formula | Explanation |
| Probability of a binomial event occurring | \(P(X=r) = \ ^n C_r p^r (1-p)^{n-r}\) | Confused? This Beginner’s Guide explains the fundamentals of binomials. |
| Notation for a binomial distribution | \(X \text{~ Bin} (n,p)\) | |
| Binomial expansion | \(P(X=x) = \binom{n}{x} p^x (1-p)^{n-x}, \ x=0, \ 1, \ . \ . \ . \ , \ n\) | |
| Expected value | \(E(X)=np\) | |
| Variance | \(\text{Var} (X) = np(1-p)\) |
Back to top
Combinatorics
| Use | Formula | Explanation |
| Permutations | \(^n P_r = \frac{n!}{(n-r)!}\) | \(n, \ r ∈ \mathbb{Z}^+\) (positive integers)
\(^n P_r\): The number of different ways you can order r items from a selection of n items. There are two things that matter: which items you pick and the order in which you pick them in. |
| Combinations | \(\binom{n}{r} = \ ^n C_r = \frac{n!}{r!(n-r)!}\) | \(n, \ r ∈ \mathbb{Z}\)
\(^n C_r\): The number of different ways you can pick r items from a selection of n items. The order of the items does NOT matter! Only which items you pick matters |
| Note: the exclamation mark (!) denotes a factorial — the product of all positive integers less than or equal to given number.
e.g. \begin{align*} |
||
Back to top
Example 25:
There are 5 cyclists participating in a race and their names are Anna, Barry, Celia, David and Edgar. The spectators are taking turns guessing who’s going to come first, second and third. How many different guesses are possible?
Solution 25:
| For simplicity’s sake, let’s refer to the cyclists by their first initial: A, B, C, D and E. If we were to pick out the order of the top 3, picking out A for 1st, B for 2nd and C for 3rd would not be the same as picking out B for 1st, A for 2nd and C for 3rd.
See how order matters in this selection? Such an ordered selection is called a permutation, and we would use the notation \(^5 P_3\) to indicate how many different permutations of the top 3 we can make from the 5 participants. We can find how many different permutations are possible by simply listing out all the different possibilities: ABC, ACB, BAC, BCA, CAB, CBA, BCD, BDC, CDB, CBD, DCB, DBC, CDE, CED, DEC, DCE, ECD, EDC, DEA, DAE, EAD, EDA, AED, ADE, … the list goes on! You can see why listing out all the permutations isn’t always the easiest way to find out how many there are. Fortunately, we can use the formula \(^n P_r = \frac{n!}{(n-r)!}\) to mathematically calculate how many permutations there are. Substitute \(n=5\) and \(r=3\) into \(^n P_r = \frac{n!}{(n-r)!}\): \begin{align*} |
Back to top
Example 26:
The prefect elections are underway at Matrix High School. In a cohort of 120 students, there are 68 female students and 52 male students. If the prefect body must consist of 30 students and an equal number of girls and boys, how many different outcomes for the prefect elections are possible?
Write your answer in scientific notation to the nearest 2 decimal places.
Solution 26:
| In this scenario, we can see that the order of the students picked to be prefects is irrelevant. The only thing that matters is the prefect body of 30 has an equal number of girls and boys.
That is, 15 female students are selected to be prefects out of the 68 in total (\(^{68} C_{15}\)) and that 15 male students are selected out of the 52 in total (\(^{52} C_{15}\)). Hence, the number of possible prefect body combinations: \begin{align*} |
Back to top
| Use | Formula | Explanation |
| Binomal theorem | \((x+a)^n = x^n +\binom{n}{1} x^{n-1} a + … + \binom{n}{r} x ^{n-r}a^r + … + a^n\) | Use this theorem to expand the powers of any expression consisting of the sum of two terms, i.e. \((x+a)^n\), where \(x\) and \(a\) can be any constant or variable, and \(n\) is a positive integer value. |
Back to top
Example 27:
Find the coefficient of \(x^3\) in the expression \((3+2x)^4\).
Solution 27:
| \begin{align*} (3-2x)^4 &= 3^4 + \binom{4}{1} 3^3 \times (-2x) + \binom{4}{2} 3^2 \times (-2x)^2+ \binom{4}{2} 3 \times (-2x)^3 + (-2x)^4 \text{ (Binomial Theorem)}\\ ∴ \text{Coefficient of }x^3 &= \frac{\binom{4}{2} 3 \times (-2x)^3}{x^3} \\ &= \binom{4}{2} 3 \times (-2)^3 \\ &= \ ^4 C _2 \times 3 \times (-8) \\ &= -144 \end{align*} |
Back to top
,