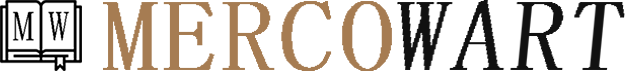In this post, we will give you the full working out and solutions to the 2021 HSC Physics Exam, written by our Head of Science Dr Alex Argyros and his team.
Find out how to answer all of the 2021 questions below!
Section 1. Multiple Choice
\(\)
| Question | Answer | Solution |
| 1 | B | The time of flight will be the same, but the range would decrease with the lower launch speed, \( s_x = u_x t \) |
| 2 | C | The force on a positive charge is in the direction of the electric field. |
| 3 | D | Protons are not fundamental particles, they are composed of three quarks. |
| 4 | B | All observers would agree on the speed of the radio waves (speed of light). The other quantities depend on the observer. |
| 5 | A | The overall shape of the spectrum resembles a black body indicating the source is a star. The wavelengths of sharply lower intensity indicate absorption lines. |
| 6 | D | He-3 has two protons and a neutron, giving a mass number of 3. |
| 7 | C | The larger current (and necessarily lower voltage) indicates a step-down transformer. The primary coil has four times more turns than the secondary coil. |
| 8 | D | The light diffracts around the disk and constructively interferes to produce the bright spot. |
| 9 | C | The potential energy decreases as the mass draws near to the stars and increases again as it moves away from them again. |
| 10 | B | Eddy currents are induced in the copper block, both ahead of the magnet and behind it. The effect of these is to produce a force to the right, following the magnet. |
| 11 | A | According to Wien’s Displacement Law \( \lambda = \frac{b}{T} = \frac{2.898 \times 10^{-3}}{310} = 9.3 \times 10^{-6} \text{ m} \) |
| 12 | D | The back EMF is proportional to the rate of change of flux through the coil, which is proportional to the angular velocity.
\( \varepsilon = -\frac{\Delta \Phi}{\Delta t} \) and \( \omega = \frac{\Delta \theta}{\Delta t} \) |
| 13 | B | \( E = \frac{hc}{\lambda} \), therefore the largest energy transition produces the shortest wavelength. |
| 14 | A | The Earth and Moon experience equal and opposite forces, causing each to accelerate towards the other with an acceleration inversely proportional to their mass. |
| 15 | C | The transmission of unpolarised light through the first polariser, \( I_1 \), would be 50% regardless of the orientation of the first polariser. \( I_2 \) depends on the angle between the two polarisers, as described by Malus’ Law. |
| 16 | B | The energy released per minute is \( 3.85 \times 10^{28} \times 60 = 2.31 \times 10^{30} \text{ J} \).
\( E = mc^2 \) indicates that this is equivalent to \( m = \frac{E}{c^2} = \frac{2.31 \times 10^{30}}{(3 \times 10^8)^2} = 2.57 \times 10^{13} \text{ kg} \). |
| 17 | C | The current in the wires will always be in opposite directions, meaning the wires will repel as per Ampere’s Law. This force will be downwards on \( X \), adding to its weight and increasing the total force on \( X \). It will be upwards on \( Y \), partially cancelling its weight, reducing the total force on \( Y \). |
| 18 | A | The charge will experience a constant force down due to its weight and a constant force to the right due to the electric field. These will add to give a constant force diagonally down and to the right, and the charge will accelerate and travel in that direction.
Opening the switch then removes the force to the right, leaving only the downwards gravitational force to act on the particle. From this point it will follow a parabolic path. |
| 19 | A | The amount of radioisotope and its activity will decrease over time due to radioactive decay. The lower number of electrons emitted due to the beta decay at the later time will result in a lower current. However the energy distribution and maximum energy of the emitted electrons remains the same, meaning the same stopping voltage will remain the same |
| 20 | D | The maximum energy of the photoelectrons will be \( K_{max} = hf – \phi \)The maximum speed of the electrons will be \( v_{max} = \sqrt{\frac{2K_{max}}{m}} \)The maximum radius will be \( r = \frac{mv}{qB} \)Substituting the velocity in the above gives \( r = \frac{m}{qB}\sqrt{\frac{2K_{max}}{m}} \) which shows that \( r \propto \sqrt{K} \).When the photon energy is \( 2\phi \), \( K_{max} = \phi \). When the photon energy is increased to \( 4\phi \), \( K_{max} = 3\phi \).Hence the maximum radius will increase by a factor of \( \sqrt{3} \). |
Question 21
a)
| \( \tau_{max} = nIAB = 1 \times 14 \times (0.1 \times 0.07) \times 0.40 = 0.0392 \text{ Nm} \) |
b) The torque is given by \( \tau = nIAB \sin{\theta} \). It will be maximum at the position shown, it will reduce to 0 after a quarter of a turn, and then increase to the maximum value after another quarter of a turn.
Question 22
The angular velocities \( \omega \) of \( X \) and \( Y \) are the same.
The instantaneous velocity of \( X \) is twice that of \( Y \), since \( X \) is twice as far away from the centre as \( Y \) and \( v = r \omega \).
Question 23
Thomson used an electric field to accelerate electrons and passed them through a magnetic field which deflected them. He then used a second electric field to balance the magnetic force on the electrons such that they did not deflect. The original amount of deflection and the strength of the electric and magnetic fields allowed him to calculate the electron’s charge-to-mass ratio.
Millikan suspended drops of oil as part of his experiment, using the electric force (from an electric field) to balance the weight of the drops (from the Earth’s gravitational field). This allowed him to measure the charge of the drops, from which he calculated the electron’s charge.
Question 24
| Initially \( \Phi = nBA = 35 \times 0.15 \times 0.02 = 0.105 \text{ Wb} \) |
\( \varepsilon = -\frac{\Delta \Phi}{\Delta t} = -\frac{-0.105}{0.4} = 0.26 \text{ V} \)
Question 25
a) The kinetic energy will increase as it accelerates to its orbital velocity.
The potential energy will increase as its altitude increases.
b) In order to stay above one position on Mars, the orbital period of the satellite must be equal to the rotation period of Mars.
Using Kepler’s 3rd Law:
| \( \frac{r^3}{T^2} = \frac{GM}{4\pi^2} \) \( r^3 = \frac{6.67 \times 10^{-11} \times 6.39 \times 10^{23}}{4\pi^2} \times (24 \times 60 \times 60 + 40 \times 60)^2 \) \( r = 2.04 \times 10^7 \text{ m} \) |
Question 26
a)
b) The student should use the line of best fit to calculate Planck’s constant. Since the equation of the graph is \( V = \frac{hf}{q_e} \), with \( V \) on the vertical axis and \( f \) on the horizontal axis, the value of the gradient will be equal to \( \frac{h}{q_e} \). The charge of an electron is known and so h can be calculated.
This method will be more reliable because the line of best fit reflects the outcome of all measurements instead of a single one.
Question 27
a)
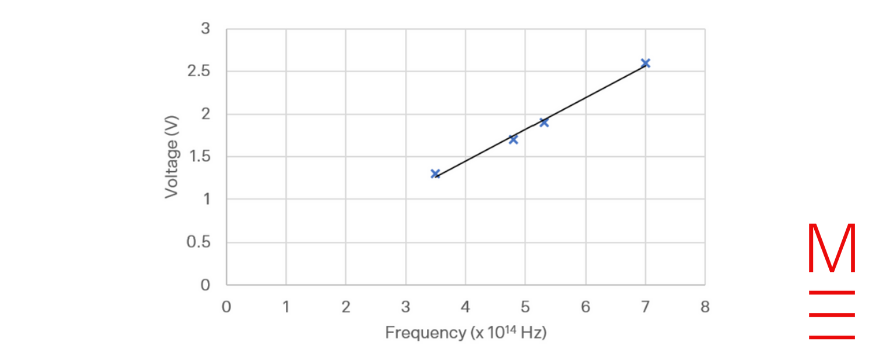
(Alternatively, the magnetic field could be into the page, and the current could be flowing to the right.)
b) The upwards force on the current-carrying rod is given by \( F = LIB \sin \theta \). Since the field is perpendicular to the current, \( \sin \theta = 1 \) and the force per unit length will be \( \frac{F}{L} = BI \).
The downwards force on the rod is its weight. The weight per unit length must equal the upwards force per unit length in order for the rod to levitate, and hence \( \frac{mg}{L} = BI \).
This gives a mass per unit length of \( \frac{m}{L} = \frac{BI}{g} \).
Substituting \( B = 1.2 \text{ T} \), \( I = 2.3 \text{ A}\), and \( g = 9.8 \text{ms}^{-2} \) gives the required value of \( 0.282 \text{ kgm}^{-1} \).
Question 28
a) The proper time for the trip is 9.4 years, and the dilated time is 15 years.
\( t_v = \frac{t_0}{\sqrt{1-\frac{v^2}{c^2}}} \)
\( 15 = \frac{9.4}{\sqrt{1-\frac{v^2}{c^2}}} \)
which gives \( v = 0.779c \)
According to an observer on Earth, the spaceship travelled \( 0.779c \times 15 \text{ years} = 11.69 \text{ light years} \) to reach the star.
b) According to special relativity, the spaceship will experience mass dilation as its speed increases, \( m_v = \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}} \). As its speed approaches the speed of light, its mass approaches infinity.
Hence, the acceleration arising from any force applied to it will approach zero and its maximum velocity will be limited to the speed of light.
Question 29
Bohr’s model of the atom was semi-classical. Even though this model introduced the concept of quantised energy levels, the electron itself was still considered to be a negatively charged particle travelling around the nucleus in circular motion.
De Broglie hypothesised that all matter including electrons had a dual wave-particle nature, with the wavelength given by \( \lambda = \frac{h}{mv} \). Electrons within an atom formed a standing wave around the nucleus, with the allowed modes corresponding to the quantised electron energy levels.
In Schrodinger’s model of the atom, electrons exist within orbitals and are described by their wavefunction. The wavefunction describes the three-dimensional probability distribution of the individual electron’s location around the nucleus. Overall the electrons behave like a cloud surrounding the nucleus.
Question 30
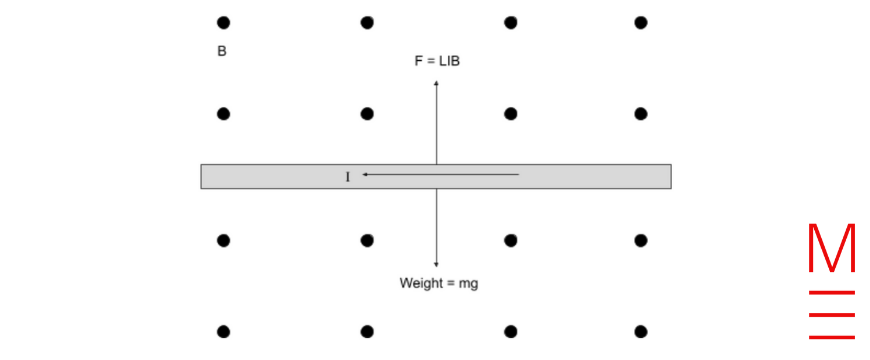
a) The electron is stationary at the beginning, meaning it has zero kinetic energy. As the potential energy decreases it is converted to kinetic energy.
b) The electron is negatively charged, so it would accelerate upwards instead of downwards in the electric field. The magnitude of the electron’s acceleration would also be greater than the proton’s. This is because the acceleration of a charged particle in an electric field is given by \( a = \frac{qE}{m} \). While the particles have the same magnitude of charge, the electron’s mass is significantly smaller. Hence, it will complete the motion in a shorter time compared to the proton.
Question 31
When the switch on cart 1 is closed, a direct current begins to flow through the circuit on that cart, passing from left to right through \( G_1 \). According to the right hand coil rule, this will result in a magnetic south pole forming on the right hand side of the cart 1 solenoid.
The solenoid on cart 2 experiences an increase in magnetic flux that points to the left. This will result in an induced EMF and current in this solenoid, according to Faraday’s Law. According to Lenz’s Law, the direction of the induced current will be such that the flux it produces opposes this increase. As a result, the second solenoid produces magnetic flux that points to the right, with an induced current that will pass right to left through \( G_2 \). A south magnetic pole is formed on the left of this solenoid.
As the two solenoids produce south magnetic poles facing each other they will repel. The forces on each cart will be equal and opposite, causing them to begin moving away from each other in opposite directions. However, since cart 1 has double the mass of cart 2, Newton’s Second law predicts that its acceleration will have half the magnitude.
Question 32
Hubble’s Law states that the recession velocity of distant objects measured from Earth is proportional to their distance from Earth, due to the expansion of space.
This model successfully demonstrates why more distant objects in space appear to be moving away from Earth at a higher velocity due to the expansion of the underlying space. If we consider \( d_1 \) to be the Earth, the distance \( (d_3 – d_1) \) will increase by a greater amount than \( (d_2 – d_1) \) in the same time frame. This will result in a larger recession velocity for the point a larger distance away, proportional to that distance.
One significant limitation of this model is that it only represents the expansion in one dimension, whereas the expansion of the universe takes place in three spatial dimensions. Another limitation is that the elastic expands within existing space, rather than representing the expansion of space itself.
Question 33
Experiment A supports the wave model of light, as it provides evidence of light undergoing diffraction and interference, which are phenomena exhibited by waves.
When the light is incident on the slits, it diffracts through each of the slits, causing curved wavefronts to emerge from both. Since the curved wavefronts now cross over one another (superimpose), the result is interference between the diffracted waves. At the screen, the places where the waves arrive in phase appear bright due to constructive interference, while places where waves arrive out of phase appear dark due to destructive interference.
Given that we know the separation of the slits and the distance to the screen, we can calculate the spacing between adjacent bright bands on the screen.
The diffraction equation is \( d \sin \theta = m \lambda \). Since the angle is small, \( \sin \theta \approx tan \theta \), and the equation becomes \( d \frac{h}{L} = m \lambda \) with \( d \) being the slit separation, \( h \) being the spacing between adjacent bright bands when \( m = 0, 1, 2… \) and \( L \) being the distance to the screen.
Hence,
| \( h = \frac{\lambda L}{d} = \frac{400 \times 10^{-9} \times 3.0}{5.0 \times 10^{-5}} = 0.024 \text{ m} = 2.4 \text{ cm} \). |
Experiment B supports the particle model of light, in which the energy carried by light is concentrated into discrete energy packets called photons with energy \( E = hf \). For light with a wavelength of \( 400 \text{ nm} \), this corresponds to a photon energy of \( E = \frac{hc}{\lambda} = 4.97 \times 10^{-19} \text{ J} \).
This can be used to explain why incident light is able to eject photoelectrons from calcium but not nickel. In the particle model of light, absorption of energy from photons only takes place if each photon has an energy above the metal’s work function (the minimum energy required to release an electron from the metal). For calcium, when these photons hit the surface, each one transfers all its energy to a single electron which can then escape with a maximum kinetic energy given by
| \( K_{max} = hf – \phi = 4.97 \times 10^{-19} – 4.60 \times 10^{-19} = 3.7 \times 10^{-20} \text{ J} \). |
For nickel, individual photons have an energy that is lower than the work function, so they will never be absorbed and the electrons stay within the metal.
Question 34
a) The kinetic energy at \( t_0 \) is dependent on the launch velocity of the projectile. It initially decreases as the projectile travels vertically upwards, because gravity does negative work on the object and kinetic energy is converted to gravitational potential energy. The minimum kinetic energy occurs at the highest point on the trajectory; this is where the vertical component of velocity reaches zero, leaving the projectile with its lowest speed overall. Finally, the projectile accelerates downwards again and the magnitude of its vertical velocity increases beyond the initial value, giving the highest kinetic energy at \( t_2 \).
b) The horizontal velocity is \( 13.76 \text{ms}^{-1} \). We can use this in conjunction with the kinetic energy to calculate the initial and final vertical velocities.
The horizontal velocity always contributes \( K = \frac{1}{2}mv_x^2 = 284 \text{ J} \).
Initially at \( t_0 \) the vertical velocity must contribute \( 864-284 = 580 \text{ J} \).
Since \( v = \sqrt{\frac{2K}{m}} \) the vertical component is \( 19.67 \text{ms}^{-1} \) upwards.
Similarly, at \( t_2 \) the vertical velocity contributes \( 1393-284 = 1190 \text{ J} \) of kinetic energy, which corresponds to a velocity of \( 27.20 \text{ ms}^{-1} \) downwards.
Now using \( v = u + at \) we can calculate the time of flight.
\( -27.20 = 19.67 + (-9.8) \times t \)
Therefore \( t = 4.78 \text{ s} \).
Question 35
a)
| In a single decay, the mass defect is \( m_{reactants} – m_{products} \).
\( 238.0495 – (234.0409 + 4.00256) = 0.006 \text{ u} \) This is equivalent to \( 0.006 \times 1.661 \times 10^{-27} = 9.966 \times 10^{-30} \text{ kg}\). According to \( E = mc^2 \) then \( E_{released} = 9.966 \times 10^-{30} \times (3 \times 10^8)^2 = 9.0 \times 10^{-13} \text{ J} \) |
b)
| The decay constant is \( \lambda = \frac{\ln 2}{t_{1/2}} = \frac{\ln 2}{87.7} = 7.9 \times 10^{-3} \text{ year}^-1 \).
After 10 years the amount of radioisotope remaining will be \( N = N_0 e^{-\lambda t} = 9.0 \times 10^{24} \times e^{-7.9 \times 10^{-3} \times 10} = 8.316 \times 10^{24} \). The number of atoms that decayed is then \( 9.0 \times 10^{24} – 8.316 \times 10^{24} = 6.839 \times 10^{23} \). Taking the energy released by each decay from part (a) gives the total energy released: \( 6.839 \times 10^{23} \times 9.0 \times 10^{13} = 6.2 \times 10^{11} \text{ J} \).
|
,